今回はメルカトル図法の距離に関するお話です。前回は緯度・経度の 1度が場所によってどれくらいの距離なのかを測りましたが、今回はメルカトル図法で示される距離の実際を検証します。
はじめに
メルカトル図法は正角図法で形は正確だが距離や面積は正確ではない
メルカトル図法は上記の特性があります。前回の記事でも触れましたが、Google Maps は 2018年8月からメルカトル図法以外に外射図法でも表示できるようになりました。これで地図の見た目は宇宙からの見た目と同じになった訳ですが、ArcGIS Online や 地理院地図など他の Web マップ サービスは依然としてメルカトル図法(Webメルカトル)が多く使用されています。
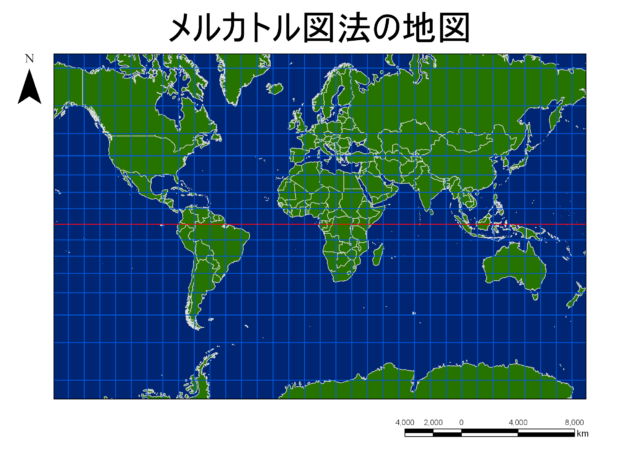
メルカトル図法を使用して、例えばこのような主題図を作成したとします。この地図には大きな問題があります。
メルカトル図法では(赤道上を除いて)距離は正しくないので、スケールバーを配置するのは不適切です。スケールバーが配置されると一般的に地図の読み手は図上どこでもスケールバーと同じ距離になると理解します。上記の地図で示されるスケールバーが正確なのは赤道上のみです。ArcGIS Online のマップ ビューアーや Google Maps でもスケールバーがありますが、これは現在表示されている地図のある場所(おそらく中心)における縮尺に基づいて動的に変化します。大縮尺で表示すれば誤差の範囲内ですが、小縮尺で表示すると正確な表示にはなりません。
メルカトル図法で示すスケールバーは正確でないと説明しましたが、どれくらい正確でないのか気になります。ということで、メルカトル図法によって示された 2点間の距離と測地線距離がどれくらい異なるのか計測してみます。
前提条件
地球の大きさには様々な定義がありますが、今回も赤道半径と極半径が異なる WGS84 楕円体を使用します。
WGS84楕円体
赤道半径:6,378,137m、扁平率の逆数:298.257223563
GCS_WGS_1984 (4326)
回転楕円体における計算式で長さを求めることもできますが、難しい計算は ArcGIS にやらせようということで今回も arcpy という API を使用して計算しました。
経度0度上で北緯0度~ 90度まで1度ずつの間隔で点を置き、その緯度経度の座標をメルカトル図法の座標に換算します。換算後の座標から東西南北に 500m 延伸させ、「東西・南北で 1km の線分」を作成します。作成した線分の測地線距離を測定します。
メルカトル図法上 1000m の測地線距離と拡大率
図法上 1000m の測地線距離を求めた結果です。メルカトル図法は緯度によって実際の距離が異なり、高緯度になると顕著に拡大率が大きくなります。89度以上は計算できないので除外しました。
Spatial Reference: World_Mercator (54004)
GCS: GCS_WGS_1984 (4326)
| 緯度 | 東西距離 (m) | 南北距離 (m) | 東西拡大率 (%) | 南北拡大率 (%) |
|---|---|---|---|---|
| 88 | 35.0167580 | 35.0167581 | 2855.7755127 | 2855.7755069 |
| 87 | 52.5115344 | 52.5115345 | 1904.3435161 | 1904.3435122 |
| 86 | 69.9899931 | 69.9899932 | 1428.7756803 | 1428.7756775 |
| 85 | 87.4467041 | 87.4467042 | 1143.5536774 | 1143.5536751 |
| 84 | 104.8762450 | 104.8762452 | 953.5047714 | 953.5047695 |
| 83 | 122.2732033 | 122.2732036 | 817.8406820 | 817.8406804 |
| 82 | 139.6321783 | 139.6321785 | 716.1672993 | 716.1672979 |
| 81 | 156.9477825 | 156.9477828 | 637.1545898 | 637.1545886 |
| 80 | 174.2146444 | 174.2146448 | 574.0045581 | 574.0045570 |
| 79 | 191.4274098 | 191.4274101 | 522.3912298 | 522.3912288 |
| 78 | 208.5807435 | 208.5807439 | 479.4306431 | 479.4306422 |
| 77 | 225.6693320 | 225.6693324 | 443.1262286 | 443.1262278 |
| 76 | 242.6878845 | 242.6878850 | 412.0518839 | 412.0518831 |
| 75 | 259.6311354 | 259.6311358 | 385.1618176 | 385.1618169 |
| 74 | 276.4938455 | 276.4938460 | 361.6717031 | 361.6717024 |
| 73 | 293.2708046 | 293.2708051 | 340.9817767 | 340.9817761 |
| 72 | 309.9568324 | 309.9568330 | 322.6255709 | 322.6255703 |
| 71 | 326.5467811 | 326.5467816 | 306.2348362 | 306.2348356 |
| 70 | 343.0355364 | 343.0355370 | 291.5149872 | 291.5149867 |
| 69 | 359.4180200 | 359.4180206 | 278.2275636 | 278.2275631 |
| 68 | 375.6891905 | 375.6891911 | 266.1774747 | 266.1774743 |
| 67 | 391.8440456 | 391.8440462 | 255.2035717 | 255.2035713 |
| 66 | 407.8776238 | 407.8776244 | 245.1715764 | 245.1715760 |
| 65 | 423.7850055 | 423.7850062 | 235.9687075 | 235.9687071 |
| 64 | 439.5613152 | 439.5613159 | 227.4995468 | 227.4995465 |
| 63 | 455.2017227 | 455.2017233 | 219.6828242 | 219.6828239 |
| 62 | 470.7014446 | 470.7014452 | 212.4488912 | 212.4488909 |
| 61 | 486.0557461 | 486.0557467 | 205.7377180 | 205.7377177 |
| 60 | 501.2599423 | 501.2599429 | 199.4972899 | 199.4972896 |
| 59 | 516.3093996 | 516.3094002 | 193.6823155 | 193.6823152 |
| 58 | 531.1995372 | 531.1995378 | 188.2531761 | 188.2531759 |
| 57 | 545.9258284 | 545.9258290 | 183.1750666 | 183.1750664 |
| 56 | 560.4838021 | 560.4838027 | 178.4172881 | 178.4172879 |
| 55 | 574.8690440 | 574.8690446 | 173.9526611 | 173.9526609 |
| 54 | 589.0771979 | 589.0771985 | 169.7570375 | 169.7570374 |
| 53 | 603.1039670 | 603.1039675 | 165.8088911 | 165.8088910 |
| 52 | 616.9451149 | 616.9451154 | 162.0889729 | 162.0889727 |
| 51 | 630.5964672 | 630.5964677 | 158.5800194 | 158.5800193 |
| 50 | 644.0539124 | 644.0539129 | 155.2665050 | 155.2665049 |
| 49 | 657.3134030 | 657.3134034 | 152.1344302 | 152.1344301 |
| 48 | 670.3709565 | 670.3709569 | 149.1711403 | 149.1711402 |
| 47 | 683.2226568 | 683.2226573 | 146.3651695 | 146.3651694 |
| 46 | 695.8646550 | 695.8646554 | 143.7061062 | 143.7061061 |
| 45 | 708.2931703 | 708.2931707 | 141.1844758 | 141.1844758 |
| 44 | 720.5044911 | 720.5044914 | 138.7916401 | 138.7916400 |
| 43 | 732.4949758 | 732.4949761 | 136.5197077 | 136.5197077 |
| 42 | 744.2610540 | 744.2610543 | 134.3614575 | 134.3614575 |
| 41 | 755.7992269 | 755.7992271 | 132.3102703 | 132.3102703 |
| 40 | 767.1060684 | 767.1060686 | 130.3600690 | 130.3600690 |
| 39 | 778.1782261 | 778.1782263 | 128.5052661 | 128.5052660 |
| 38 | 789.0124216 | 789.0124217 | 126.7407170 | 126.7407169 |
| 37 | 799.6054515 | 799.6054516 | 125.0616786 | 125.0616786 |
| 36 | 809.9541881 | 809.9541882 | 123.4637730 | 123.4637730 |
| 35 | 820.0555803 | 820.0555802 | 121.9429541 | 121.9429541 |
| 34 | 829.9066535 | 829.9066535 | 120.4954793 | 120.4954793 |
| 33 | 839.5045113 | 839.5045112 | 119.1178828 | 119.1178828 |
| 32 | 848.8463352 | 848.8463351 | 117.8069526 | 117.8069526 |
| 31 | 857.9293856 | 857.9293855 | 116.5597095 | 116.5597096 |
| 30 | 866.7510024 | 866.7510021 | 115.3733884 | 115.3733884 |
| 29 | 875.3086050 | 875.3086047 | 114.2454209 | 114.2454209 |
| 28 | 883.5996935 | 883.5996932 | 113.1734209 | 113.1734209 |
| 27 | 891.6218489 | 891.6218485 | 112.1551700 | 112.1551700 |
| 26 | 899.3727332 | 899.3727328 | 111.1886055 | 111.1886055 |
| 25 | 906.8500902 | 906.8500898 | 110.2718091 | 110.2718091 |
| 24 | 914.0517460 | 914.0517455 | 109.4029965 | 109.4029966 |
| 23 | 920.9756089 | 920.9756084 | 108.5805086 | 108.5805086 |
| 22 | 927.6196704 | 927.6196699 | 107.8028024 | 107.8028024 |
| 21 | 933.9820050 | 933.9820044 | 107.0684440 | 107.0684441 |
| 20 | 940.0607706 | 940.0607700 | 106.3761016 | 106.3761016 |
| 19 | 945.8542091 | 945.8542085 | 105.7245388 | 105.7245388 |
| 18 | 951.3606465 | 951.3606458 | 105.1126094 | 105.1126094 |
| 17 | 956.5784931 | 956.5784923 | 104.5392518 | 104.5392519 |
| 16 | 961.5062437 | 961.5062430 | 104.0034848 | 104.0034849 |
| 15 | 966.1424782 | 966.1424774 | 103.5044026 | 103.5044026 |
| 14 | 970.4858614 | 970.4858606 | 103.0411714 | 103.0411715 |
| 13 | 974.5351433 | 974.5351425 | 102.6130260 | 102.6130261 |
| 12 | 978.2891595 | 978.2891586 | 102.2192662 | 102.2192663 |
| 11 | 981.7468310 | 981.7468301 | 101.8592542 | 101.8592543 |
| 10 | 984.9071648 | 984.9071639 | 101.5324120 | 101.5324121 |
| 9 | 987.7692536 | 987.7692527 | 101.2382190 | 101.2382191 |
| 8 | 990.3322763 | 990.3322753 | 100.9762101 | 100.9762102 |
| 7 | 992.5954977 | 992.5954967 | 100.7459738 | 100.7459739 |
| 6 | 994.5582691 | 994.5582681 | 100.5471505 | 100.5471506 |
| 5 | 996.2200280 | 996.2200270 | 100.3794314 | 100.3794315 |
| 4 | 997.5802983 | 997.5802973 | 100.2425571 | 100.2425572 |
| 3 | 998.6386904 | 998.6386894 | 100.1363165 | 100.1363166 |
| 2 | 999.3949014 | 999.3949003 | 100.0605465 | 100.0605466 |
| 1 | 999.8487145 | 999.8487135 | 100.0151308 | 100.0151309 |
| 0 | 1000.0000000 | 999.9999990 | 100.0000000 | 100.0000001 |
メルカトル図法の誤解
メルカトル図法の緯度に対する拡大率は余弦からこのように求められます。
緯度(φ) 上の拡大率 = 1/cos(φ)
0°:1
60°:2
75°:2.9238
80°:5.7588
85°:11.4737
仮に「メルカトル図法は地球に円筒を被せて中心から光を当てた影」でできるとすると、そんなにゆるやかな拡大率はとはなりません。これについては以下の書籍で解説されています。
『地図投影法』P45 column4 地図投影法についてよくある間違い
地図投影法に関して広まっている誤解の筆頭は、メルカトル図法の原理に関するものであろう。球に円筒を巻きつけて球の中心から投影すればメルカトル図法が得られるという解説や図解は、学生用参考書や一般向けの地図に関する書籍によく見られるものであるが、間違いである。こうして得られる投影は心射円筒図法であってメルカトル図法ではない。
私もこの書籍を読んではじめて誤りに気づきました。メルカトル図法の計算式はこちらに記載があります。
まとめ
計測した結果、緯度25度くらいまでは1割程度、36度あたりで2割の拡大率で、60度になるとほぼ2倍となり、高緯度になるほど顕著に拡大率が大きくなりました。そのため、メルカトル図法は距離や面積の測定には不向きだということが分かります。また、同一地点で東西と南北の拡大比率はほとんど同じです。このことから、メルカトル図法は歪みが少ない(形状は正確)ということが分かります。
2年ほど前「意外と日本って大きい。」というタイトルで The True Size Of... サイトを紹介し、ネットで盛り上がりましたがあのタイトルはナンセンスです。メルカトル図法は北にいくほど拡大されるのだから日本が大きくなるのは当たり前です。比較するなら赤道に移動させ「ロシアって意外と小さい。」というタイトルにするべきでしょう(ロシアは面積世界一なので赤道に移動しても大きいんだけど)。
ソースコード
Python ウィンドウにそのまま貼り付けてご利用ください。ArcMap 10.4、AcGIS Pro 1.3、ArcGIS Pro 2.2 で動作確認しております。arcpy.SpatialReference の引数である EPSG 番号を変更して一般的に使用される球体としての地球で計算することもできます。
#coding:UTF-8
# メルカトル図法の指定距離における測地線距離
# 経度0度、北緯0度~90度を中心に東西・南北の指定距離を
# 測地線距離に換算して比較
# ArcGIS Pro 1.3,ArcGIS Pro 2.2, ArcMap 10.4.1 で動作確認
import arcpy
import copy
# WGS84楕円体
# 赤道半径:6,378,137m、扁平率の逆数:298.257223563
# GCS_WGS_1984 (4326)
gcs = arcpy.SpatialReference(4326)
#gcs = arcpy.SpatialReference(4035) # 地球半径 Authalic Shpere GCS_Shpere GCS_Sphere (4035)
# メルカトル図法
pcs = arcpy.SpatialReference(54004)
# 測定係数
ratio = 1000 # (m)
print("Spatial Reference: {0} ({1})".format(pcs.PCSName, pcs.PCSCode))
print(" GCS: {0} ({1})\n".format(gcs.GCSName, gcs.GCSCode))
print("メルカトル図法上 {}m の測地線距離\n".format(ratio))
print("{}\t{}\t{}\t{}\t{}".format("緯度", "東西距離 (m)".ljust(10), "南北距離 (m)".ljust(10), "東西誇張率 (%)".ljust(10), "南北誇張率 (%)".ljust(10)))
for lat in range(88, -1, -1):
# 中心点を投影変換
point = arcpy.Point(0, lat)
point_gcs = arcpy.PointGeometry(point, gcs)
point_pcs = point_gcs.projectAs(pcs)
# 東西長
point_width_from = copy.copy(point_pcs.trueCentroid)
point_width_to = copy.copy(point_pcs.trueCentroid)
point_width_to.X += 1 * ratio
polyline_width = arcpy.Polyline(arcpy.Array([point_width_from, point_width_to]), pcs)
length_width = polyline_width.getLength("GEODESIC")
# 南北長
point_height_from = copy.copy(point_pcs.trueCentroid)
point_height_from.Y -= 0.5 * ratio
point_height_to = copy.copy(point_pcs.trueCentroid)
point_height_to.Y += 0.5 * ratio
polyline_height = arcpy.Polyline(arcpy.Array([point_height_from, point_height_to]), pcs)
length_height = polyline_height.getLength("GEODESIC")
print("{:0=2}\t{:0=13.7f}\t{:0=13.7f}\t{:0=13.7f}\t{:0=13.7f}".format(lat, length_width, length_height, ratio / length_width * 100, ratio / length_height * 100))