横メルカトル図法の詳しい解説

はじめに

2021年9月末から Twitter に #一日一図法と称して毎日1つの図法を掲載しはじめました。Twitter に書ける短文の範囲で解説していますが、横メルカトル図法は要点がいろいろあるのでこの記事で補足します。

横メルカトル図法とは

メルカトル図法は正角図法で、高緯度ほど面積の拡大率が顕著になります。しかし、赤道上は正確で、一定の低緯度内であれば面積の歪みを無視することができます。そこで、メルカトル図法（縦軸法）を横軸法にして、中央子午線付近で面積の歪を抑えたのが横メルカトル図法 (Transverse Mercator projection) です。ドイツの数学者（科学者）であるランベルトが1772年に発表しました。

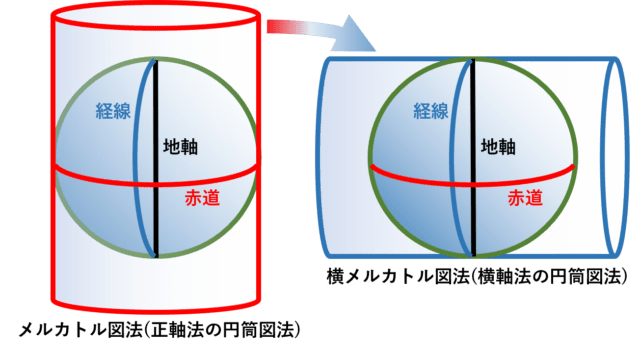
ランベルトが考案した計算式は地球を真球とみなしたものでしたが、その後 1822年にドイツの数学者（科学者）であるガウス が回転楕円体 での導入式を考案しました。しかしガウスはこの投影法について発表しなかったため、その全容が知られることはありませんでしたが、ドイツのクリューゲルがガウスの遺稿を整理し、1912年に発表しました。

ガウスと名が付く地図投影法は複数ありますが、計算式が異なり、展開される形状も異なるそうです（政春 2000）。

• ガウス・クリューゲル図法（ガウス正角図法）
• ガウス正角二重図法
• ガウス・シュライバー図法（ガウスの等角二重投影法）：ドイツのシュライバーが開発し、1876年から測量のためにプロイセンで使われた

後述の UTM図法や平面直角座標系にはガウス・クリューゲル図法が使われています。日本でも 1884年から 1954年までは平面直角座標系にガウス等角二重投影法が使われていたそうです（現在は「等角」は非推奨の用語で「正角」という）。1952年に国土調査法施行令と、1954年の建設省告示でガウス・クリューゲル図法に移行しています（政春 2011 p.177）。

また、元々ランベルトが発明した横メルカトル図法は回転楕円体である地球を真球として導く計算式でしたが、英語圏では回転楕円体による求め方も含めて「横メルカトル図法」と呼び、ドイツでは「ガウス・クリューゲル図法」と呼ぶそうです。そのため、GIS ソフトウェアで定義されている EPSG をみても、UTM図法の地図投影法は横メルカトル図法 (Transverse Mercator) と定義されています。これはガウス・クリューゲル図法と同等とみなして問題ありません。

ユニバーサル横メルカトル (UTM) 図法とUTM座標系

横メルカトル図法の特徴を活かして、世界的に体系化したのが「ユニバーサル横メルカトル図法」略して「UTM図法」です。

UTM図法は「図法」と書かれていますが、メルカトル図法や横メルカトルと対等な関係にある地図投影法ではありません。ガウス・クリューゲル図法を使って国際準則に従って作られてたものを意味するので、特に GIS を扱う立場なら「UTM座標系」と理解した方が分かりやすいと考えます。現在でも地図学の専門書や国土地理院の立場での解説では「UTM図法 (projection)」と説明されていますが、GIS の立場で説明された解説では「UTM座標系 (coordinate system)」と示される傾向にあります。

なお、地図学の大家である野村正七先生の文献（1974 p.101）を読むと、見出しが「UTM座標系」となっており、横メルカトル図法を使った一定のルールに基づいて定めたものと解説した上で、「これをUTM図法（Universal Transverse Mercator's projection）と名付けた」と 説明されています。さらに、経度6度の範囲に分割された地域範囲と定められた中央子午線を説明した上で、UTM座標系という、と説明されています。筆者には野村先生の解説による用語の使い分けが正しく理解できてませんが、意図的に用語を使い分けれられているようです。

また、"「横メルカトル図法」では中央子午線上の長さの歪みはないが、「UTM図法」では中央子午線上の長さの歪みが0.9996ある」"と説明されていますが、GISソフトウェアでは横メルカトル図法（Transverse Mercator Projection）のパラメーターとして、中央子午線上の縮尺係数を指定することができるので、必ずしも横メルカトル図法で中央子午線上に長さの歪みがない（＝縮尺係数が1）とは限りません。

「図法」か「座標系」かは元の英文である projection の訳に関連していますが、GIS で本格的に座標系や地図投影法を操作すると突き当たる大きな壁で、「座標系」や「地図投影法」といった用語を知り、知識を深めていくほど混乱します。ここでは GIS を使用する立場から「座標系」を意味した解説として「UTM」と表記します。

UTM の歴史

文献からの引用です。

UTM座標系：ソビエト連邦では、1935年以来、80°N以南の地域を横メルカトル図法によって地図に描いていたが、1つの中央経線を基として東西方向に投影する範囲をそれぞれ経度3°と定めていた。第2次世界大戦中、アメリカ合衆国・ソビエト連邦・イギリス・フランスなどの連合国側は共同作戦の便宜上、ソビエト連邦の制度を取り入れ、一定のルールに従って横メルカトル図法の地図を作ることにし 、これを UTM図法 (Universal Transverse Mercator's Projection) と名付けた。我が国の国土地理院は戦後、昭和35年（注：1960年）7月、これ以降大きな縮尺の地形図は UTM図法によることを決定し、UTM図法に対応する日本語としてユニバーサル横メルカトル図法の名をあてることにした。

野村 1974 p.101

自国の国土を覆う大きな縮尺の地図作成にガウス・クリューゲル図法を用いることに先鞭をつけたのはドイツで1927年であった。1935年にはソ連もこれに従った。

第2次世界大戦中、連合国は各国がまちまちの図式の地図を使用していることから生ずる作戦上の不便を痛感した結果、戦後1950年代の初頭に北大西洋条約機構 (NATO) に加盟している国の間で、一定の約束をし、ガウス・クリューゲル図法で地図を作成することを取り決めた。

野村 1983

UTM図法は1947年頃にアメリカ軍が採用したものであるが、その後世界各国で主に中縮尺の地形図に使われるようになった。日本では、昭和30年（注：1955年）式5万分1地形図図式からそれまでの多面体図法に代えて UTM図法を採用することになったが、実際の地形図がこの投影法に置き換わるには時間を要した。

政春 2011

本題から逸れますが、興味深い一節。

日本の地形図では、肝心のU.T.M.座標がどこにも示されていませんので、U.T.M.を使っている意味がありません。

その方眼座標が示されていないのは、示す地図がすべて軍用地図であるという解釈から、日本の地形図ではそれを使ってはならないという国会の決議あったためです。これは、できあがった地図の上に任意の方眼をかぶせて大砲の弾の落ちる位置を計算した第1次世界大戦以来の座標の使い方の1つを問題にしたのでしょう。しかし、これはまったくのナンセンスではないでしょうか。地図が軍事目的に利用されては困ると考えるのでしたら、地図の販売を禁止するしかありません。

五百沢 1995 p.28

UTMの仕組み

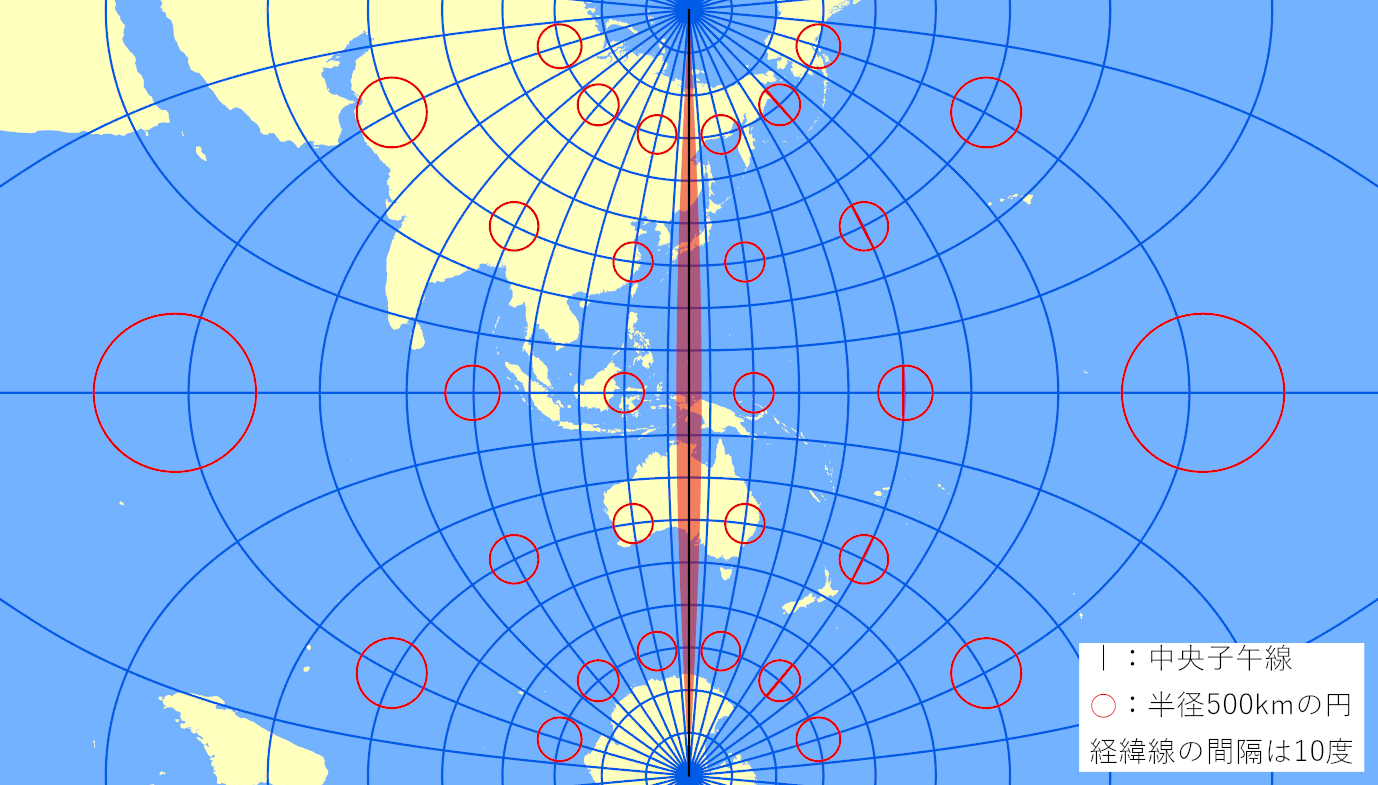
UTMは、中央子午線から東西 3度ずつの 6度幅を1つのゾーン（座標帯）として、世界を 60のゾーンに分けています。たとえば関西付近は、中央子午線を東経135度に設定した「ゾーン53」に含まれています。

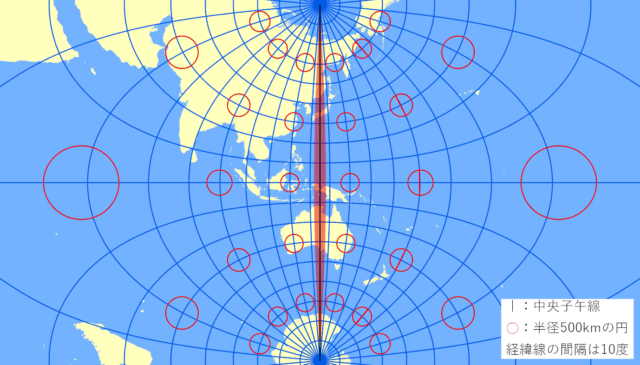
ゾーンはさらに北半球と南半球で分かれているので、合計120のゾーンがあります。横メルカトル図法は極まで表現することができますが、UTMの適用範囲は北緯84度から何位80度までと決められています。当初の北限は北緯80度までと決められていましたが、グリーンランドの北端やロシア、カナダの当処分をカバーするために後から北限が伸びました。UTMでカバーしきれない北極圏と南極圏は、別途用意されているユニバーサル極心平射図法（UPS図法）［座標系］が用意されています。

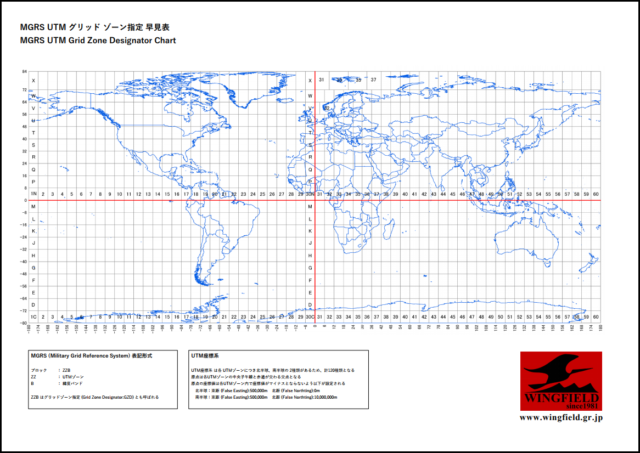
横メルカトル図法は、中央子午線上が最も距離・面積の歪みがなくて、東西に離れるほど歪みが大きくなる。そこで、UTMでは全体に 0.9996という一律の「係数」を掛け合わせています。こうすることで、縮尺係数を一定以内に収めることができます。

縮尺とは実際の地球に対する地図上の距離比と習いますが、厳密には地図は図法によってその場所での比は違います。たとえばメルカトル図法で「縮尺 1:xxxxxx」と1つの値のみが示されている場合、その縮尺値は赤道上の値を示していることになり、緯度60度では2倍に拡大されていることになります。地球をを縮小した地球儀を平面に展開すると仮定した際の、地球儀の縮尺を基準縮尺 (nominal scale) といいます。縮尺係数 (scale factor) とは、地図上のその場所における基準縮尺に対する比です。

UTM は、全体に 0.9996 という「係数」（※注：縮尺係数とは異なります）を掛け合わせることで、結果的に中央子午線上の縮尺係数が 0.9996 となり、日本付近では中央子午線から東西に約180km で縮尺係数が 1 となり、東西に約255km 離れたところで縮尺係数が 1.0004 となります。

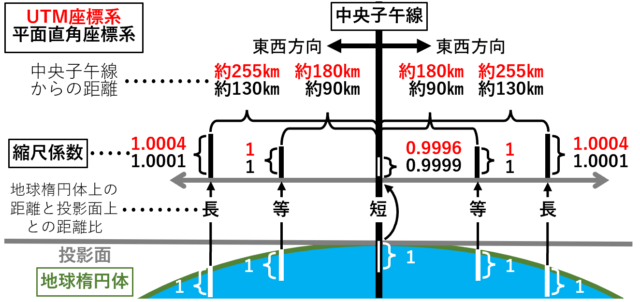
UTM の縮尺係数を解説した書籍では、「東西約270km 離れた場所で 1.0006」という解説が見られますが、これは日本付近に限定したものと思われます。赤道の長さは 40,075km なので、60で割ると 1つのゾーンは最大で中央子午線から 334km 離れることになります。334km 離れた場所での縮尺係数は 1.001 です。つまり最大で 0.1% 歪むことになります。

なお、ここでいう距離は投影座標での平面距離を意味します。縮尺係数は NOAA のサイトで計算できます。

また、UTM図法のイメージ図として、縮尺係数を説明するために割円筒図法として描かれているものがありますが、あくまで接円筒図法で求められた結果に対して一定の係数を掛け合わせて、適用されるゾーン内での距離（面積）歪みを一定以内に抑えると考えるのが適切です。割円筒という図解では真実は表せないので、数式で考えるべきです。

UTM は中縮尺地図（20万分の1～1万分の1）で使われています。

平面直角座標系

縮尺係数が 0.9996～1.001 ということは、1000m の長さが最大で1001mの歪みがあるということです。そこで、同じ横メルカトル図法を使って中央子午線を日本付近に複数設定し、縮尺係数が 0.9999 から 1.0001 の範囲に収まるように定義したのが「平面直角座標系」です。これは日本固有の座標系で、地図に掛け合わせる係数を 0.9999 とし、中央子午線上の縮尺係数が 0.9999、中央子午線から東西約90km離れたところで縮尺係数が1、約180km離れたところで 1.0001 となります。平面直角座標系は原点が 19箇所あり、基本的に都道府県ごとに適用される「系」が異なります。

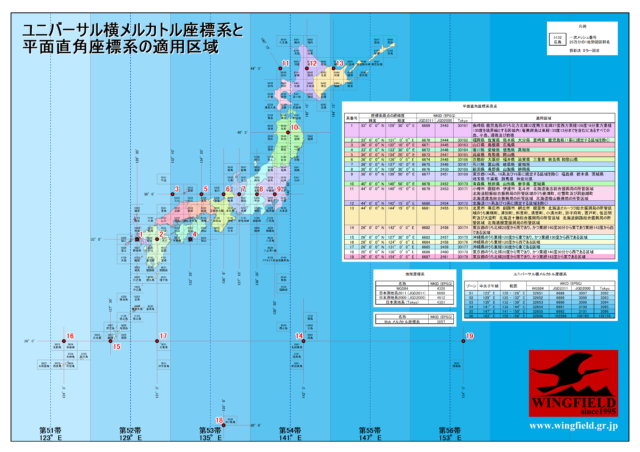
「UTMは捉え方が線で、平面直角座標系は面」という説明を見ることがありますが、両者の考え方はまったく同じです。しかし、固有名詞がUTMは「UTM図法」なのに対して、平面直角座標系は「座標系」となっています。

平面直角座標系は大縮尺地図（1万分の1～250分の1）で使用されています。

ガウス・クリューゲル座標系

「ガウス・クリューゲル図法」は、UTM と同様に、地図投影法以外の、座標系の名称としても使われていて、東ヨーロッパでは日本の平面直角座標系に相当する、各国のローカルな座標系を意味する場合もあります。その体系は UTM と似ています。

投影座標

横メルカトル図法には次のパラメーターがあります。

• 中央子午線 (central meridian)：地図の中心にあたる経度を設定、中央子午線の経線は直線となる。投影座標における X軸の原点にあたる経度。
• 縮尺係数 (scale factor)：地図全体に掛け合わせる係数で、結果的に中央子午線上における縮尺係数の数値
• 原点の緯度 (latitude of origin)：投影座標における Y軸の原点にあたる緯度。
• 東距 (false easting)：投影座標の X軸における原点の数値。
• 北距 (false northing)：投影座標の Y軸における原点の数値。

原点の緯度、東距、北距は地図の見た目に影響を与えないパラメーターです。投影された地図本来の座標は、地理座標（緯度経度）ではなく、投影座標という、原点からの距離で示した座標値です。

UTMの原点は、赤道と、それぞれの座標帯の中央子午線に当たる場所ですが、原点の座標値は (0、0 ではなく東距と北距を設定しており、北半球の場合は (500,000， 0)、南半球の場合は (500,000 ，10,000,000) としてゾーン内の投影座標が常に正になるように工夫されています。

平面直角座標系の原点の座標値は (0、0) ですが、法律上の定義では南北方向が X軸で、それに直交する方向を Y軸としています。数値からジオメトリに変換する際は、列名の意味を理解刷る必要があります。

ArcGIS の地図投影法における「横メルカトル図法」

ArcGIS がサポートする横メルカトル図法には 2種類があります。

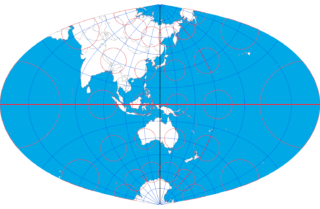
• 横メルカトル図法 (Transverse Mercator)
• ガウス・クリューゲル図法 (Gauss Kruger)

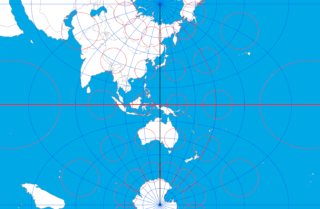
ヘルプを読んでも違いよく分かりませんでしたが、Esriテクニカルサポートの回答によると、この 2つの地図投影法で使われている内部の計算式は同じとのこと。横メルカトル図法であっても回転楕円体もサポートされています。また、以下の 2つも同じガウス・クリューゲル図法ですが、より中央子午線から離れた範囲も表示できるように計算式が調整されたものです。

• 横メルカトル図法 (Transverse Mercator Complex)
• 横メルカトル図法 (Transverse Mercator NGA 2014)

また、ArcGIS Desktop 10.3までのヘルプにはサポートされている地図投影法のトピックとして「ユニバーサル横メルカトル図法」がありましたが、序盤で説明したように図法と座標系との混乱をさけるためか、以降のバージョンのヘルプには項目が存在しません。

まとめ

横メルカトル図法について、専門書で説明されている、GISエンジニアや知っているべき情報を網羅しました。情報満載でなので困惑した場合は、たとえば 2ステップで理解を深めると良いでしょう。

• 高校地理
  • メルカトル図法は赤道付近の面積歪みは少ないので、円筒図法の投影面を横にして（横軸法）投影面と接する地図の中心（中央子午線）付近を正確に表現したもの。
  • 横メルカトル図法にすると赤道から極まで正しく表現できるが、地図の中心から東西に離れるほど面積の歪みが大きくなる
  • そこで全世界を表現できるように、経度6度刻みで地図の中心を決めて体系化した。これが「ユニバーサル横メルカトル図法」略して「UTM図法」
  • 国土地理院の地形図など、中縮尺地図に採用されている
• GISを扱う大学生・エンジニア
  • 名称としては「UTM図法」というが、歴史的な経緯で英語の名称をそのまま翻訳したので「図法」とよばれている
  • GISを扱うなら「UTM座標系」と理解したほうがわかりやすい
  • （地図投影法に各種パラメーターがあることを理解した上で）
  • 北距のために、北半球と南半球でも異なるゾーン（座標帯）となる
  • ArcGIS では、横メルカトル図法とガウス・クリューゲル図法は同一のもの
  • UTM における「縮尺係数」はあくまで地図上で計測によって求められるもの、GISソフトウェアで設定する「縮尺係数」は誤解を与えている。これは地図全体に掛け合わせるための一定「係数」で、結果として中央子午線上の縮尺係数を示しているにすぎない
  • 割円筒という図解では係数の真実は表せないから数式で考えるべき
  • ガウスが導いた横メルカトル図法は複数があるが、UTMも平面直角座標系も、ガウス・クリューゲル図法が使われている
  • 英語圏ではガウス・クリューゲル図法を含めて「横メルカトル図法」という
  • ドイツでは「ガウス・クリューゲル図法」というが、日本の平面直角座標系に相当する「ガウス・クリューゲル座標系」も存在するので、"Gauss=Kruger" の使われ方にも注意が必要

参考文献

• 野村正七 (1974)『指導のための地図の理解』中共出版
• 野村正七 (1983) 『地図投影法』財団法人日本地図センター
• 五百沢智也 (1995)『2万5千分の1図による最新地形図入門』山と溪谷社
• 政春尋志 (2000)「ガウス=クリューゲル法とガウス正角二重法について」地図 Vol.38 No.3
• 政春尋志 (2011)『地図投影法－地理空間情報の技法』朝倉書店
• 羽田康祐 (2021)『地図リテラシー入門－図の正しい読み方・描き方がわかる』