心射円筒図法とメルカトル図法の違いを ArcGIS で地図投影して理解する

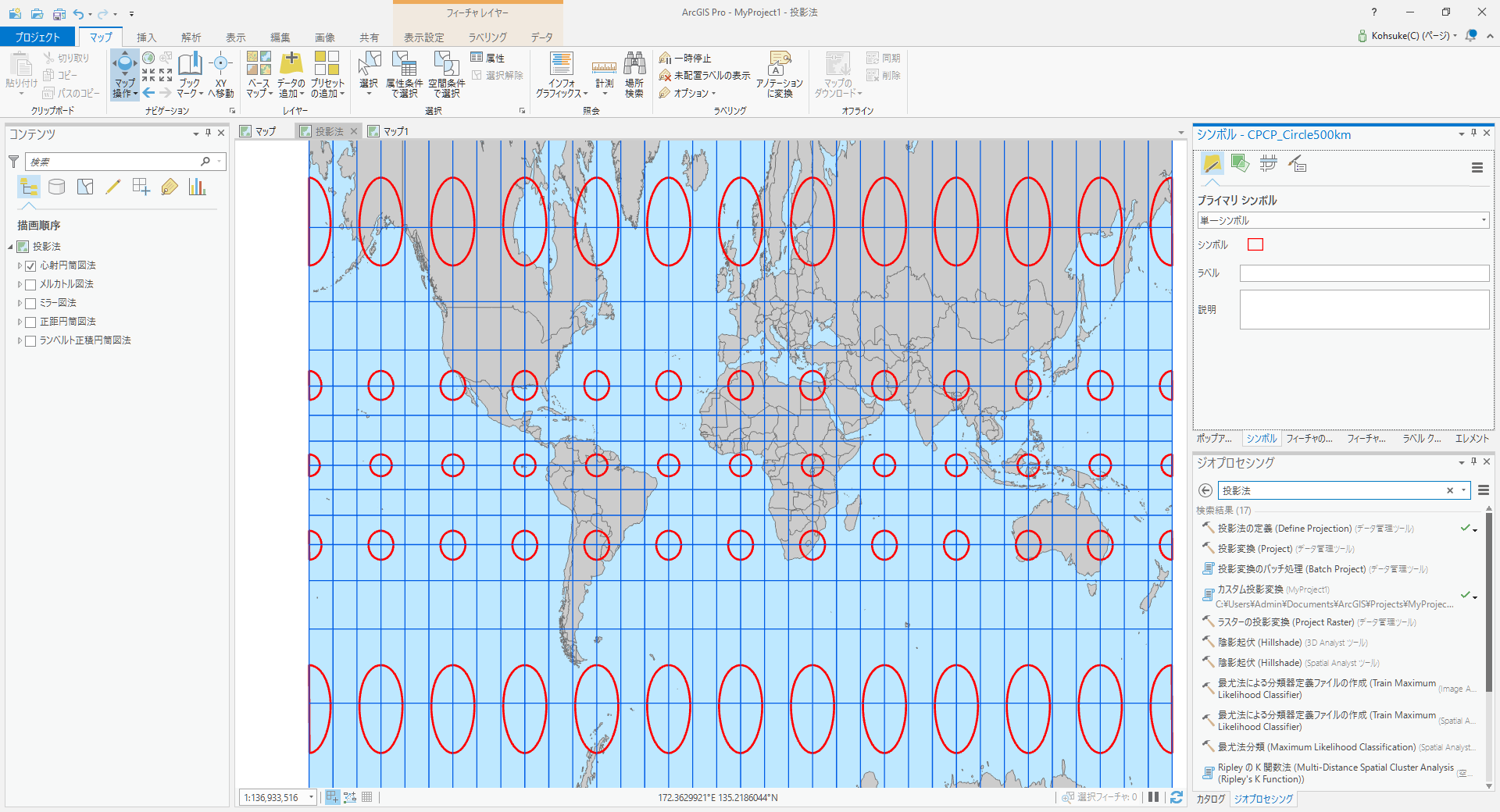
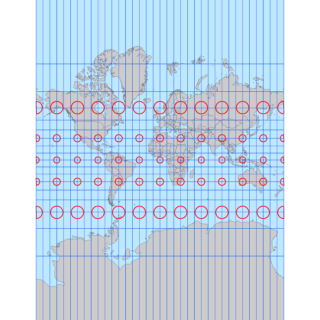
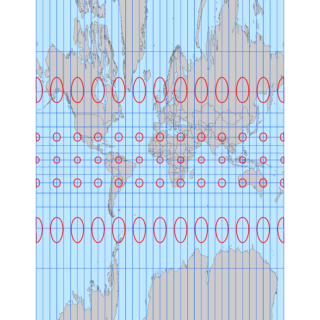
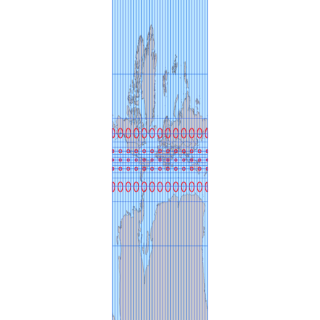
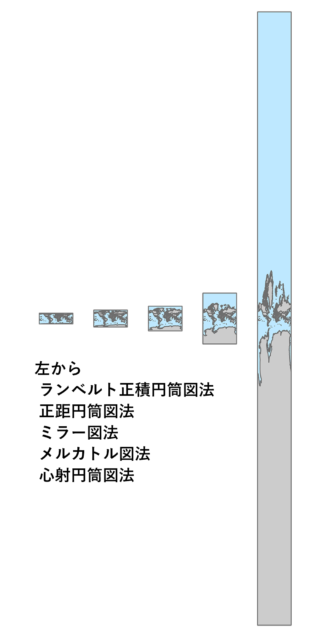
メルカトル図法の誤解を解くシリーズ第3段です。前回は心射円筒図法がどれくらい縦長に投影されるかを作図によって求めましたが、実際に地図で表現した方が分かりやすいので独自に心射円筒図法を作成して確認しました。

ArcGIS では現時点で心射円筒図法がサポートされていないため、地理座標系の緯度経度から投影座標系の XY座標に換算する式を作成し、ジオメトリの座標値を直接書き換える方法で処理して実現しています。

円筒図法

代表的な円筒図法です。まずはこれら 5つの投影法の計算式をプログラミングして座標値を換算し、地図を作成しました。

• ランベルト正積円筒図法
  正射円筒図法ともいうことができる図法。緯度は無限の彼方からスクリーンに光を平行に当てたのに等しい。
• 正距円筒図法
  標準緯線を赤道にすると緯度1度と経度1度が等しい距離になる。
• ミラー図法
  メルカトル図法に設定する緯度を 0.8倍し、結果を0.8で割ることで緯度方向の拡大率を緩やかにし、極の表現を可能とした。
• メルカトル図法
  緯度をランベルト関数（グーデルマン関数の逆関数）で計算して求めた正角図法。
• 心射円筒図法（英語）
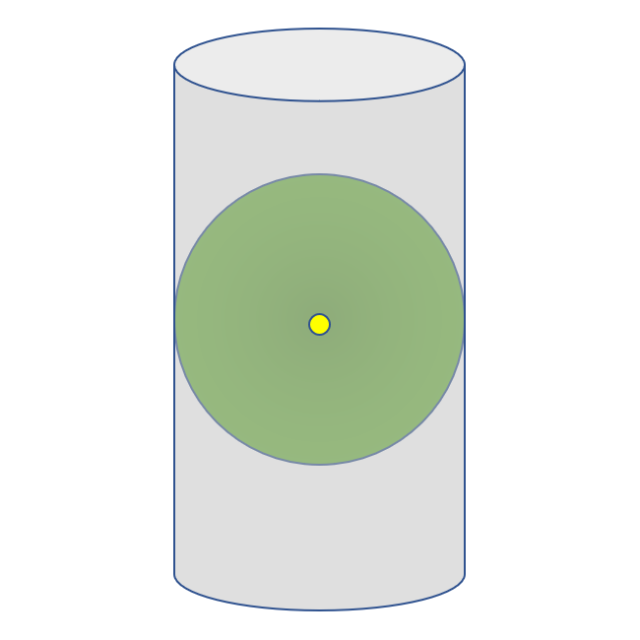
  地球に円筒を被せて中心から光を当てた際の円筒に映る影に等しい。

地図の比較

実際に投影変換した地図を見てみましょう。経線方向の長さは同じですが、緯線方向は極に向かって拡大率が異なります。

地図の比較 (2)

心射円筒図法でグリーンランドがすべて表示される縮尺で表示。かなり縦長となり、心射円筒図法だと緯度60度くらいから相当無理が出てきます。

横に並べて比較

緯度89°まで表現して比較した図です。心射円筒図法の拡大率は半端ないです。ランベルト正積円筒図法、正距円筒図法、ミラー図法は両極点を表示することができますが、メルカトル図法、心射円筒図法は計算式の特性上極点の座標を求めることはできません。

緯度の拡大率を比較

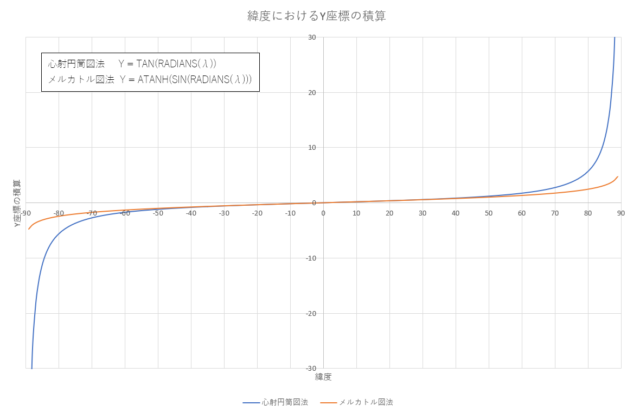
緯度の拡大率をグラフで可視化

よく円筒をイメージして両極点は影が映し出せないと説明していますが、それは tan90度の解が出せないためです。メルカトル図法は双曲線関数というものを使って計算するのですが、これも 90度だと解が出せないので投影できません。

メルカトル図法を円筒で説明するなら、高緯度になるほど光源が円筒側に近づく、とすれば正しい説明になるのではないでしょうか。

円筒図法の模式図

心射円筒図法とメルカトル図法の緯度の拡大率をグラフで可視化しました。心射円筒図法は 60度を超えたあたりから極端にY座標が大きくなるのに対して、メルカトル図法は緩やかな曲線であることが分かります。89.999999 と 90 に近付くほど顕著になります。

緯度におけるY座標の積算

• Excel ワークシート

メルカトル図法は、Google Maps の登場で緯度 85度までが表示される（グリーンランドがすべて表示される）までは、北緯80度まで（グリーンランドが切れている）の図ばかりを見てきました（メルカトルも 1550年に発表した主図は北緯80度～南緯66度だった）。円筒に光の影を当てると80度以上は表現が無理だからと思っていました。これもメルカトル図法が円筒に映し出された影だと誤解してきた要因ではないかと考えます。

メルカトル図法は、南北89度でも赤道周長の 2倍以下の長さで表現はできます。心射円筒図法は一目で地図が引き延ばされていると分かるぐらい拡大されています。

処理方法

5つの投影法の座標値を換算する関数を定義し、[カスタム投影変換] ツールを作成して処理しました。今回は ArcGIS Pro の arcpy で処理しましたが、ArcMap の arcpy でも同じコードで処理できます。ただし、現在理解できているのは地球を球とした場合だけなので、回転楕円体は考慮していません世界全体を表示する縮尺なら地球楕円体は球として計算しても問題ありません（地図と測量のQ&A Q50 (2013) より）。

ArcGIS は「心射円筒図法」を認識できないので、他の投影法が定義されたデータと正しい位置関係で重ね合わせることはできません。そのため、変換したデータの座標系は「未定義」としてください。（未定義に設定できるのは ArcMap のみ）。赤道半径を 180/π に設定すると、地理座標系のデータと正しい位置関係で表示できます。ただし、緯度が 90 を超えるので ArcGIS 上ではおかしな認識となるため、すべての座標系を「未定義」とするのがベターです。

arcpy で書いたコードです。スクリプト ツールとして設定できるように書かれていますので興味がある方は試してみてください。

• カスタム投影変換ツール用コード

コード内の投影座標の計算に用いる関数がこのように異なります。

#lat=緯度, radius=地球半径, y = 投影Y座標
y = math.tan(math.radians(lat)) * radius	# 心射円筒図法
y = math.atanh(math.sin(math.radians(lat)))* radius	# メルカトル図法
y = math.atanh(math.sin(math.radians(lat* 0.8))) * radius / 0.8	# ミラー図法
y = lat / math.degrees(1) * radius		# 正距円筒図法
y = math.sin(math.radians(lat)) * radius	# ランベルト正積円筒図法

まとめ

ティソーの指示楕円が円にならなければ正角図法とはいえません。上記の 5つの投影法のうち、地球上に描いた円が地図上でも円となっているのはメルカトル図法だけとなります。ただし円の半径が大きくなると円の北端と南端とで拡大率が違うため、上の図のように半径 500km と大きな円を描くと高緯度ほど歪みが大きくなります。

メルカトル図法は等角航路と絡めた説明が出てきますが、等角航路が直線で描けるのは①経線が平行である、②正角図法である、の 2つの条件を同時に満たす必要があるため、メルカトル図法だけが等角航路を直線で描くことができず投影法ということになります。

最後に、「メルカトル図法は形は正しいが距離や面積が間違っている。」と覚えてきましたが、間違っているは緯度30度を超えたあたりから顕著に拡大されるためで、赤道上は正確です。メルカトル図法が面積比較のために使われることはありませんが、緯度10度以内なら小縮尺図では誤差の範囲内と言えるでしょう。

メルカトル図法の地図を見ただけで考えるとうまく理解できませんでしたが、心射円筒図法の地図と比較すれば誤解が解消できました。

実際に地図で描いて確認するのが一番分かりやすいですね。