目次
はじめに
「小縮尺地図なら地球を球と見なして描いてもよい」という記述
地図と測量の Q&A(2013 年 5 月発行版)の Q50 (39 ページ) で、以下のように記述されています。

Q50
地図投影は、どんなときでも地球を楕円体として計算しなければならないのか?
A50
作図する地図が小縮尺の場合、地球を球として計算しても良いことになっています。この場合、どの縮尺からを、小縮尺と考えるのかが問題となっています。
地球を球として計算する場合は、その半径を地球楕円体の3軸 (X Y Z) 半径の平均とすることが、通常の地図作成で行われています。日本の測量法では GRS80 地球楕円体を3軸半径の平均をとって 6,371.0km としています。過去においてベッセル地球楕円体の 3軸半径の平均は 6,370.3km としていた時代もあります。
次に、日本の領土とその周辺の地域を対象とする場合と、地球表面の全域あるいは極、赤道を含む阪急程度を対象範囲とする場合の二つに分けて考えてみます。
(1)日本の領土とその周辺の地域を対象範囲とする場合
対象範囲を、具体的に北緯20度~21度、東経120度~160度と仮定します。地球楕円体の子午線長は、北緯20度~21度で 110.7106km、49~50度で111.2194km です。一方、球の場合の子午線長はどこでも 1度差で 11.1949km です。これによると、低緯度の方で球との差が大きくその値は 484m です。これを、縮尺かすると 100万分の1 で 0.484mm、500万分の1 で 0.097mm ですから、地図上で無視できる誤差を 0.1mm までとするなら、おおよそ 500 万分の 1 以下の小縮尺の地図の場合は球として扱っても良いと考えられます。
(2)地球表面全域あるいは極、赤道を含む半球程度を対象とする範囲の場合
地球楕円体の子午線長は、緯度0~1度で 111.5744km、89度~90度で 111.6939km です。球としたときの子午線長は前の (1) に記したとおりですから、球との差の値は最大で 620.5m となります。これを縮尺化すると 600 万分の 1 で 0.103mm、700 万分の 1 で 0.089mm ですから、おおよそ 700 万分の 1 以下の小縮尺の地図の場合は球としても扱っても良いとの結論になります。
電子地図は紙地図の縮尺の考え方がそのまま適用できる訳ではありませんが、ディスプレイ上で人間が認識できる最小の線幅が 0.1mm とするなら、同じ考え方で良いでしょう。だだし、多くの GIS ソフトは 96dpi 相当で縮尺表示されています。最近のディスプレイは高解像度化しており96dpi 以上のものが一般的です。また、ディスプレイスケーリングの設定によっても値が変わりますので気をつけましょう。これは別の記事で詳しく説明しています。
本当に700万分1以下の縮尺なら世界地図を球とみなして問題ないのか
当初 700万分1 という縮尺がピンときていなかったので鵜呑みにしてしまいましたが、計算できなくても実際に地図表示するとよくわかります。実際に700万分の1の縮尺で紙に世界地図を表現して確認しました。実際の用紙に印刷することはできないので、ArcGIS Pro のレイアウトを使ってディスプレイ上に仮想の用紙を定義しました。すると、そもそも700万分の1の縮尺でメルカトル図法で世界の範囲(南極を除く)を描くには、幅575cm * 高さ445cm の用紙が必要なことが分かりました。人物影を置いて比較するとこのようになります。
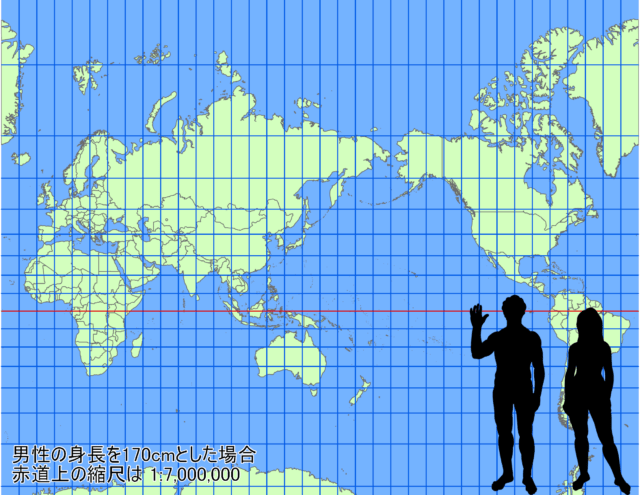
部屋には貼れないくらいのとんでもない大きさです。
そして北海道を拡大すると、通常の WGS84楕円体として地図を表現した場合と、赤道半径を半径とした球で地図を表現した場合とでは、赤道上での縮尺が700万分の1だと北海道宗谷岬は 5mm もずれて表示されます。下の画像は用紙レイアウトに配置した地図ですが、ルーラーと表示縮尺を確認してみてください。
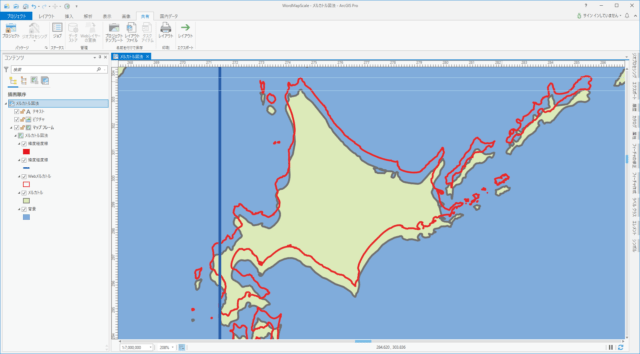
疑問
ここで『地図と測量のQ&A』 QA50 に書かれていた「0.1mm 以内」に収まっておらず、説明と食い違っていることに気づきます。
解説では根拠として描く範囲の北端1度の距離差と、南端1度の距離差を比較し、南端側の距離差がより大きくなるので、この距離差を元に計算しています。長さを比べた距離が 1度だから該当の縮尺で 0.1mm 未満という結果になっていますが、比率を比べるのであれば1分でも1秒でもよいといえます。同じ理屈で、南端の緯度1秒(約30m)の距離同士を比較すれば差は非常に微々たるものとなり、もっと大きな縮尺で表現しても問題ないことなります。
回転楕円体の扱い
地球を平面の地図に表現するには、①地理座標を測量して②地図投影します。①で求められる地理座標は測地系によって決まります。測地系とは地球の大きさが定義された回転楕円体と地球(ジオイド)との重心位置を定めたものです。②は地理座標という角度由来の値をXY軸の距離が均等な投影座標に換算することです。このとき計算に使われる角度を回転楕円体として展開するのか球として展開するのかによって、実際に地図投影される地図の形が変わってきます。
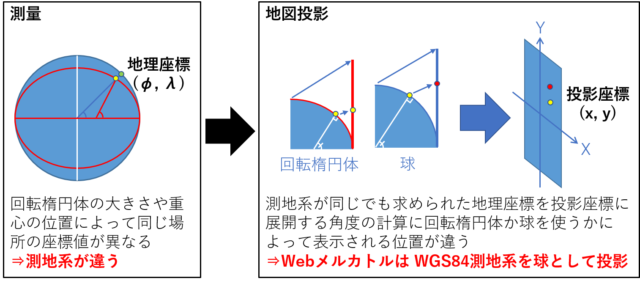
測量
緯度経度を測る回転楕円体(これを準拠楕円体といいます)が完全な球体だと、いわゆる「測地系が異なる」状態になってしまうので、同じ場所を示す座標が変わってしまいます。Googleマップで求められる地図上の地理座標は WGS84 の値なので、測量は回転楕円体に基づいて求められているということができます。
地図投影
こちらは、投影法によって異なり、元々球を前提にした投影しかできないものもあります。例えば、正方形図法 (plate carree) は緯度1度と経度1度を等しい距離の直交座標で表現するので、準拠楕円体がどんなに扁平した回転楕円体であっても球とみなして投影されます。
正方形図法に似た正距円筒図法 (equidistant cylindrical) は、球とみなして投影するか、回転楕円体として投影するかの選択肢があり、両者を比べると地図上の子午線の長さが変わってきます。
メルカトル図法は、たとえば ArcGIS の場合では、バージョン9.2 までは測地系の準拠楕円体に基づいた投影しかサポートされていませんでしたが、バージョン9.3から投影法のオプションとして真球に基づいた投影 (auxially sphere) もサポートされるようになりました。
その背景は Googleマップの登場にありますが、Googleマップは地理座標を真球と見なして投影しています。以前、Webメルカトル座標系を解説した記事で「Esri の Webメルカトルは座標系は投影法の力で測地系を変えた」と解説していましたが、これは適切な説明ではありませんでした。地図投影する際に使う回転楕円体が球とみなされている、と説明するのが適切でした。地球を扱う回転楕円体は、測量の場合と、地図投影の場合とで分けて考えると意味の違いが整理できます。
検証
では一般的に使われる準拠楕円体に基づく地理座標を球と見なして地図投影して良い縮尺は何分の一以下なのかを改めて考えます。今回は Googleマップを例として WGS84楕円体とします。WGS84楕円体はGRS80楕円体と比べて極半径が 0.1mm 長いだけなので数値的には同じものと見なして問題ありません。
| WGS84楕円体 | 半径 (m) | 周長 (m) | 緯度90度間の距離 (m) | 緯度30度間の距離 (m) | 緯度1度間の距離 (m) |
|---|---|---|---|---|---|
| 赤道半径 | 6,378,137.000 | 40,075,016.686 | 10,018,754.171 | 3,339,584.724 | 111,319.4908 |
| 極半径 | 6,356,752.314 | 39,940,652.742 | 9,985,163.186 | 3,328,387.729 | 110,946.2576 |
| 3軸平均半径 | 6,371,008.771 | 40,030,228.704 | 10,007,557.176 | 3,335,852.392 | 111,195.0797 |
| 赤道半径による球 | 6,378,137.000 | 40,075,016.686 | 10,018,754.171 | 3,339,584.724 | 111319.4908 |
| 極周長と3軸平均周長の差 | 14,256.457 | 89,575.962 | 22,393.991 | 7,464.664 | 248.822 |
なお、国際海里(ノーティカルマイル)は(赤道周長+極周長)÷2の1分相当の距離として求められましたが、3次元の球は2軸ではなく3軸の平均をとるべきなので、(赤道周長+赤道周長+極周長)÷3で求めます。
世界地図で球とみなして表現してもよい縮尺
地球を真球と見なしてもよい地図の縮尺は、地図の北端と南端の距離差で比較するべきで、赤道を挟むなら赤道(緯度0度)から表現したい緯度までの幅で比較するべきだと考えます。世界地図ならば、緯度0度から北緯90度までの距離の差を測るということです。
赤道から極までの緯線の長さは以下のとおりです。
- 緯度差:90度
- 回転楕円体(WGS84)の場合 :9,985km
- 球(WGS84の3軸平均)の場合:10,008km
- 差:22.4km
- 差が図上0.1mm以下になる縮尺:1:223,939,910 (約2億2千4百万の1)
これは子午線を引き延ばすことなく展開した場合の計算なので、メルカトル図法のようにさらに引き延ばしいている場合はより小さな縮尺にしなければいけないでしょう。
世界地図で球とみなして表現してもよい縮尺(Googleマップの場合)
Googleマップの投影法に使われている半径は3軸の平均ではなく赤道半径なので 6,378.1km です。これで世界地図を表示する場合として計算すると以下のようになりました。
- 回転楕円体(WGS84)の場合 :9,985km
- 球(WGS84の赤道半径)の場合:10,019km
- 差:約11.2km
- 差が図上0.1mm以下になる縮尺:1:335,909,858(3億3千6百万分の1)
日本地図で球とみなして表現してもよい縮尺
差は赤道が0で緯度差が広がるほど累積します。地図に表示する範囲が中緯度・高緯度であれば、その一番緯度の低い地点から差を積算して考えます。
日本のように一部の範囲で考えるなら、北緯20~50度の緯度30度の距離を比較するべきでしょう。同様に計算すると次のようになります。日本の北端と南端は地球1周の12分の1の長さと考えます。
- 緯度差30度
- 回転楕円体(WGS84)の場合 : 3,328km
- 球(WGS84の3軸平均)の場合:3,336km
- 差:約7.5km
- 差が図上0.1mm以下になる縮尺:1:74,646,640(7千5百万分の1)
回転楕円体の場合は、同一経線上の緯度差は低緯度ほど短く、高緯度ほど長くなり、「緯度1度間の距離」は赤道付近と極付近とでは最大で1kmの差があります。ここで求めた「緯度1度間の距離」は平均値を使用しました。平均値であっても「日本の領土とその周辺の地域を対象範囲とする場合、おおよそ500万分の1以下の小縮尺の地図の場合は球として扱っても良い」の説明が成り立たないことを証明するには十分な誤差です。
まとめ
世界範囲の地図を表現するなら地図投影は回転楕円体として扱わなければならない、ということになります。日本地図のように地図に表す緯度間の範囲が狭くなる場合は、図幅内で見えている範囲での相対的な位置関係があっていれば良いので、7千5百万分の1までは問題ないことになります。この縮尺もかなり小さいので、いずれにしてもB5版の地図帳に表示される地図の縮尺であれば、すべて回転楕円体として扱うべきだという結論になります。
しかし、Googleマップを見ただけで地球の扱いが回転楕円体ではなく球だと気づける人はいませんし、たとえ紙地図の上で 1cm の違いがあったとしても直感的に見分けられる人はいないでしょう。
GIS だと縮尺はディスプレイ上でいくらでも拡大できますし、ディスプレイの大きさによって実際の縮尺も変わってきます。文中の縮尺値はあくまで人物の身長が170cmの場合を想定しているので、この画面に見えている地図そのものの縮尺値ではないことを理解してください。


参考
ArcGIS のサポートする地図投影法のパラメーター
ArcGIS for Desktop ヘルプでサポートされている投影法の解説を読んでいると、いくつかの投影法で「球面上でのみサポート」と書かれたページがあります。たとえば「エケルト図法(第 4 図法)」の下部にこの記述が書かれています。
以前、これの意味がよく分からなくて上司と話題になった際に、Esri フォーラム のスレッドに書かれているのを見つけてもらいました。
Projections identified as "sphere-only" only use a radius value from a sphere. If you use a projected coordinate system that's based upon a geographic coordinate system that uses a spheroid (ellipsoid), we use the semimajor axis as the sphere's radius.
Esri の Projection 関連のスペシャリストである、Melita Kennedy さんの投稿から解釈すると、「球面上でのみサポート」と記載されている投影法の場合、座標系に回転楕円体を指定しても投影は球体として扱われ、楕円体の長半径が球体の半径として使用される、とのこと。
さらにヘルプの続きを読むと、ArcGIS には同じ投影法でもパラメーターが異なる 2種類があります。たとえば先ほどの「エケルト図法(第 4 図法)」では
- False Easting(東距)
- False Northing(北距)
- Central Meridian(中央子午線)
の 3 つのパラメーターを持つのですが、「エケルト第 4 図法球体補正(Desktop version 9.3 以降)」では、
- False Easting(東距)
- False Northing(北距)
- Central Meridian(中央子午線)
- Auxiliary Sphere Type(球体補正タイプ)
と 4 つのパラメーターになっています。
実際に ArcMap で [投影座標系プロパティ] ダイアログを開くと、いくつかの投影法には「~_Auxiliary_Sphere」と書かれたものが加わっていることが分かります。
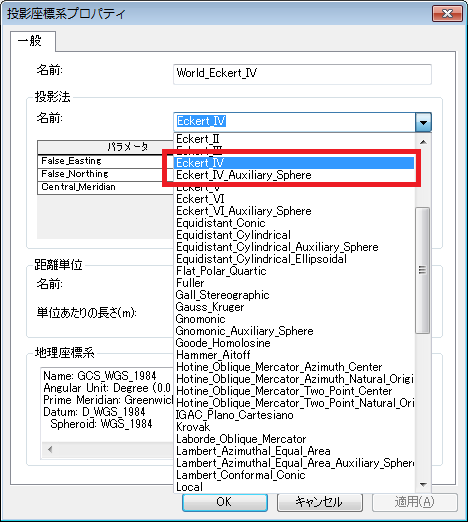
「~_Auxiliary_Sphere」という投影法はバージョン 9.3 から登場したもので、こちらを選択することで球体の半径を以下の 4 つオプションから選択できるようになります。
Auxiliary Sphere Type パラメータには、0(地理座標系の長半径または半径を使用)、1(短半径または半径を使用)、2(正積半径を計算して使用)、または 3(正積半径を使用し、測地緯度を正積緯度に変換)を指定できます。
原文)The Auxiliary Sphere Type parameter accepts 0 (use semimajor axis or radius of the geographic coordinate system), 1 (use semiminor axis or radius), 2 (calculate and use authalic radius), or 3 (use authalic radius and convert geodetic latitudes to authalic latitudes).
訳語は原文を忠実に訳しているのですが、訳語の意味が理解できなかったので英語に詳しい人に聞くと「原文が "or" ではなく "as" の間違いじゃないの?」と言われました。as と読めば
- 0:地理座標系の長半径を半径として使用
- 1:短半径を半径として使用
- 2:正積半径を計算して使用
- 3:正積半径を使用し、測地緯度を正積緯度に変換
ということで意味が理解できます。前述のフォーラム スレッドでも、Melita さんは "as" を使われてます。あと「正積半径(authalic radius)」「測地緯度(geodetic latitudes)」「正積緯度(authalic latitudes)」についても調べたはずなんだけど、手元に情報が残ってなかったので後日追記しておきます。正積半径については Wikipedia に書かれてました。
ArcGIS はすべての地図投影法で回転楕円体による計算をしていますが、同一名称で後ろに "~Auxiliary_Sphere" と書かれている地図投影法では、回転楕円体を球とみなして計算しているので、小縮尺地図なら、"~Auxiliary_Sphere" を使用しても問題ありません。
そもそもこの「Auxiliary Sphere Type」なるパラメーターは Google Maps の登場によって必要に迫られて作られました。これまでの ArcGIS や それ以前の Esri 製品でも地球を球とみなしたメルカトル図法を作ることは当然できましたが、従来の方法だと普通の人にとっては困ったことが起きたのです。詳しくは別の記事で解説しています。