GIS 界隈にいると、たまに耳にする「地理学は(儲からないから)役に立たない」という辛辣なお言葉。このように言われた時に言い返せるパワーワードが、「だからWebメルカトルなんてものがつくられたんだ」です。今では当たり前に使われている Webメルカトルですが、理解を深めるほどなんでこんなものを作ったのだろうと感じてきます。2005年、Goole Maps の登場で日の目を見るようになり20年近くが経ちましたが、今やこの問題点が指摘されることはありません。今回は禁忌に触れていきます。
目次
「Webメルカトル」は地図投影法の名前ではない
よく「Webメルカトル図法」と言われますが、Webメルカトルは測地系の要素も含まれているので、単なる投影法ではなく座標系(座標参照系)です。
単語の初出は Esri で、 日本語では「Webメルカトル図法」と訳されてはいますが、Coordinate Systems の中にリストされているので「座標系」というのが妥当と考えます。 ArcGIS の定義では次のように定められています。
- 名前:Web Mercator (auxiliary sphere) (WGS 1984) [Webメルカトル (球体補正) (WGS84)]
- 投影法:Mercator Auxiliary Sphere [メルカトル球体補正]
- 測地系:WGS 1984 [WGS84]
おそらく「UTM図法」と同じ感覚で使われているのだと思いますが、私は「Webメルカトル図法」と言いたくないので「Webメルカトル」とぼかした表現を多用しています。「UTM図法」という用語は国土地理院で使われていますし、高校地理でも習うので疑問を持つことはないでしょうが、GISに造詣を深めていくと、ソフトウェアの投影法の一覧に「UTM Projection」は出てこないことをしります。UTM図法は歴史的な経緯でその名前が付けられ、訳された単語ですが、GISユーザーとしては「UTM座標系」でないと矛盾が出てきます。この用語は GIS をより詳しく理解する課程で必ず当たる障壁だと思っています。この辺の話は別の機会でとりあげます。
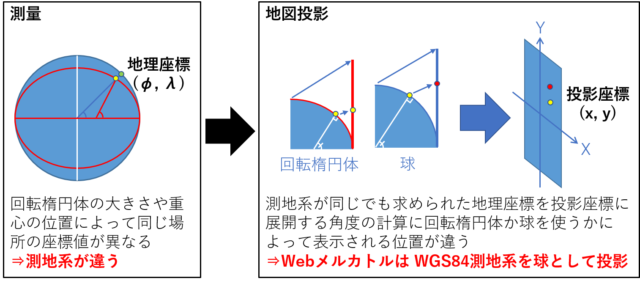
本題に戻り、「Webメルカトル」という名称で定義されているのは、測地系が「WGS84(回転楕円体)」で、投影法が「メルカトル球体補正」である、ということです。「球体補正」とは、地球が回転楕円体であっても、球と見なして投影するというものです。
地球を球とみなして捉えればよい時には深く考える必要はありませんが、測量や GIS で扱う地球は、赤道方向にやや膨らんだ、回転楕円体とみなして緯度経度を決めています。この膨らんだ状態を扁平しているといい、その割合を扁平率といいます。
測量で使用している地球の大きさでは、赤道半径と極半径の差が約21km、赤道周長と極周長の差が約67kmあります。そのため、地球を完全な球としてとらえて地図に投影すると、本来示すべき位置がずれてきます。
Google Maps が定義(買収前の Where 2 Technologies 時点でかもしれません)した座標系は、なぜか極半径を赤道半径と同じ大きさの球としたメルカトル図法で投影しました。小縮尺地図のみを表すならこの差は無視しても問題ありませんが、Google Maps では、大縮尺地図まで画一的にメルカトル図法で表現されます(最近は小縮尺で外射図法で表現する設定もあります)。そのため、従来の測量に基づいて作られた地図をそのまま重ねようとすると、中緯度~高緯度では最大で 20km 以上ものズレが生じることになりました。
この辺については以前記事にまとめたので併せてご覧ください。
角度が正しい「正角図法」とは
正角図法は地図上のどこでも角度が正しいという意味ですが、それは、(微細な範囲で)地球上に描いた円が地図上でも円の形状を維持できるということです。
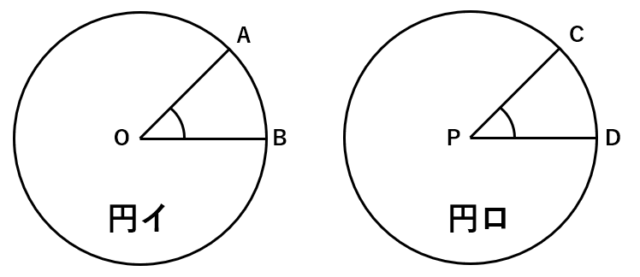
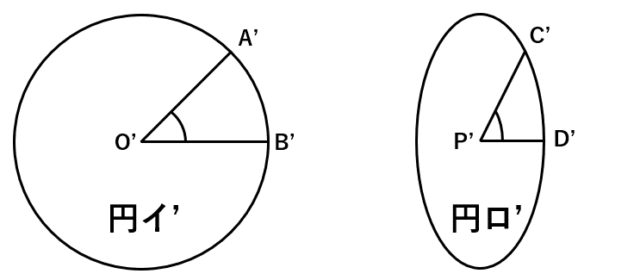
メルカトル図法は、高緯度の面積歪みは大きいものの、角度が正しく示せる正角図法です。そのため、地球が扁平していたら、投影する際も扁平率を考慮しなければいけません。ところが、Google が定義した、Webメルカトルは、WGS84 という回転楕円体上で計測したの緯度経度を球とみたてて投影するため、実際の地球よりも南北に引き伸ばされてしまいます。本来より余計に引き延ばされるので角度が正しくないのです。
実際の地球の半径や周長が数十km 違うといっても扁平率は 1/298 と微細です。文書だけで説明してもイメージしにくいので、極端に偏平したモデルを使って確認してみます。
扁平率 1/3 のモデルで考える
同じ緯度経度に大陸や島があると仮定した、扁平率が 1/3 の地球を定義しました。
- 赤道半径:637,8137m
- 極半径:4252091.333333334m
- 扁平率:1/3
ArcGIS では扁平率が 1/2 の準拠楕円体も定義して地図に表現することはできるのですが、確認用に点から正確な半径1,000km の円を作成するバッファーの処理がうまくできなかったので 1/3 に留めました。
ローカル図法
扁平率 1/3 の地球を無限の彼方から望遠鏡で眺めると、このような形状になります。誰が見ても赤道方向に引き伸ばされている(南北に潰れている)ことが分かります。これはローカル図法ですが、地球を真下に見下ろした地点にある円は、円の形状がほぼ維持できています。
赤の円は、扁平率 1/3 の地球上に描いた半径1,000km の円です(扁平率が極端に大きいためか、形状が若干怪しいです)。
正方形図法
この地球を正方形図法で表現します。正方形図法は緯度1度と経度1度を同じ距離で直角に交わり表現されるので、扁平率にかかわらず同じ形状になります。
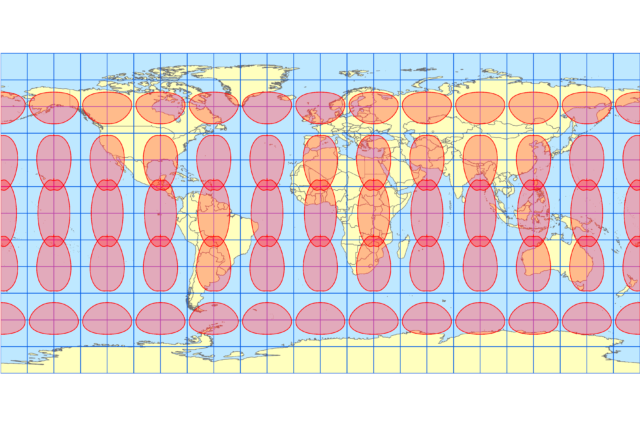
正方形図法で実際の地球(WGS84 楕円体)に半径 1,000km の円を描くと、以下のようになります。極端に扁平した地球だと、地図に描いた円の形状はかなり歪みます。
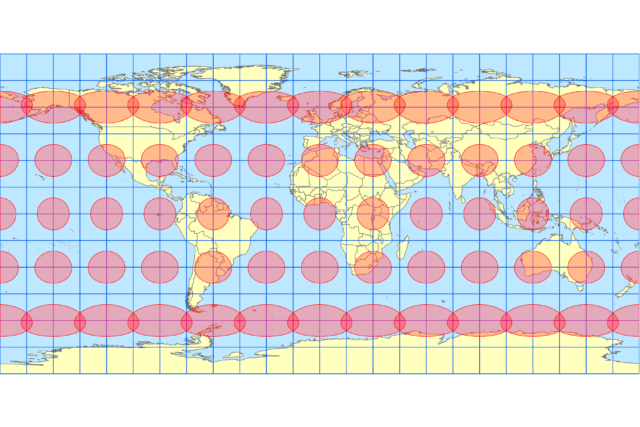
正距円筒図法(回転楕円体を考慮)
正距円筒図法で投影してみます。正距円筒図法で正距なのは、赤道と同一経度の長さという意味しますが、数式の種類により、回転楕円体を考慮せずに表現をするもの(=正方形図法)と、回転楕円体を考慮したものがあります。後者で示すと、以下の図のようになります。赤道付近では、円の形状が維持できていますが、地図自体は南北に大きく潰れています。
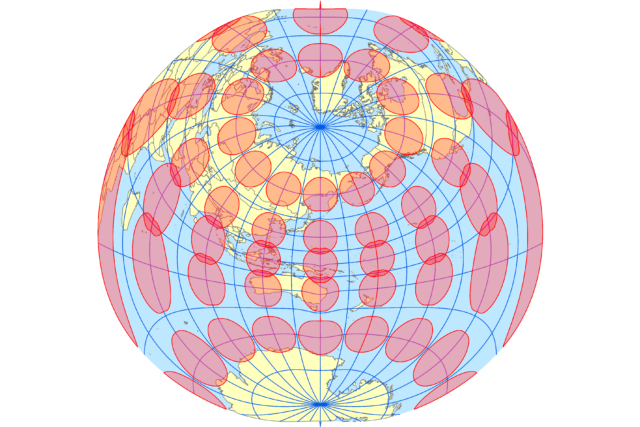
正距方位図法
正距方位図法で投影すると、図の中心が北極点・南極点の場合を除いて、対蹠点が真円ではなくなります。
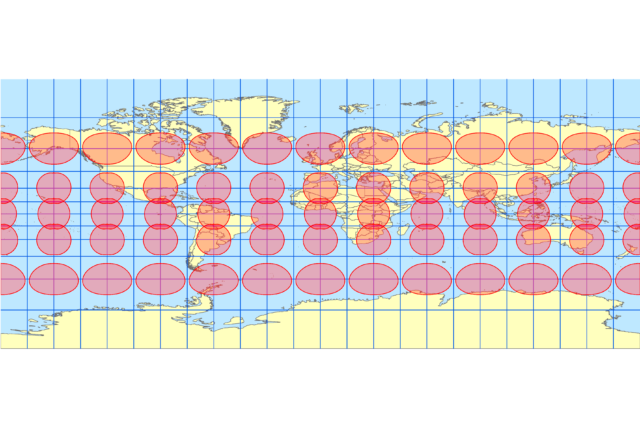
メルカトル図法
本題の、メルカトル図法で投影するとこのようになります。
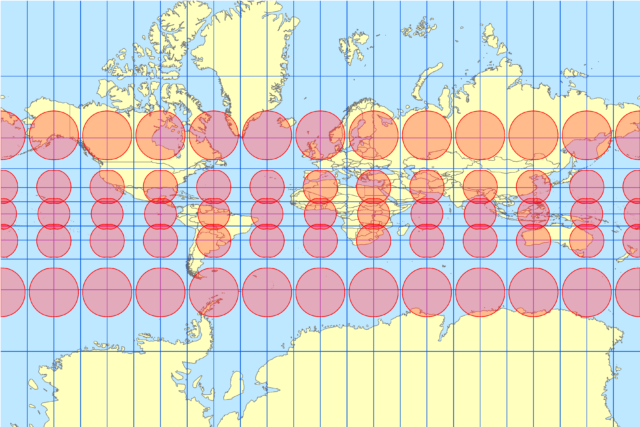
地球が大きく扁平しているので、メルカトル図法でも南北が縮んだ表現になります。低緯度では、正距円筒図法と似た表現となり、高緯度ほど緯線の拡大率分だけ経線も引き伸ばされます。メルカトル図法は回転楕円体の場合はそれを考慮して投影するので、円の形状は円のまま維持されます。つまり正角です。
横メルカトル図法
国土地理院の地形図や都市計画図などの大縮尺地図で使われている横メルカトル図法で表現すると下のようになります。横メルカトル図法も正角図法なので、円の形状が維持されています。
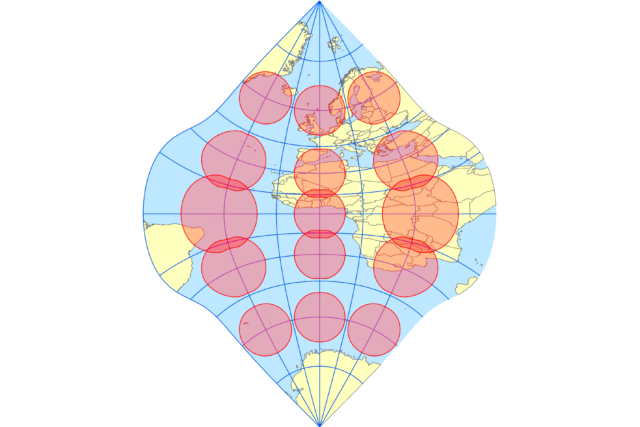
横メルカトル図法は、ランベルトが作成した図法ですが、ランベルト自身が発明した図法では地球の扁平率は考慮されていませんでした。その後、ガウスが回転楕円体に対応した式を作成し、クリューゲルがガウスの遺稿を発表して世の中に認知されます。ArcGIS など、GISソフトに定義されている「横メルカトル図法」は、扁平率も考慮した「ガウス・クリューゲル図法」と同等のものであると考えてください。
ガウス・クリューゲル図法は正角なので、上記の地図も、円が円の形状を維持できています。
Webメルカトル
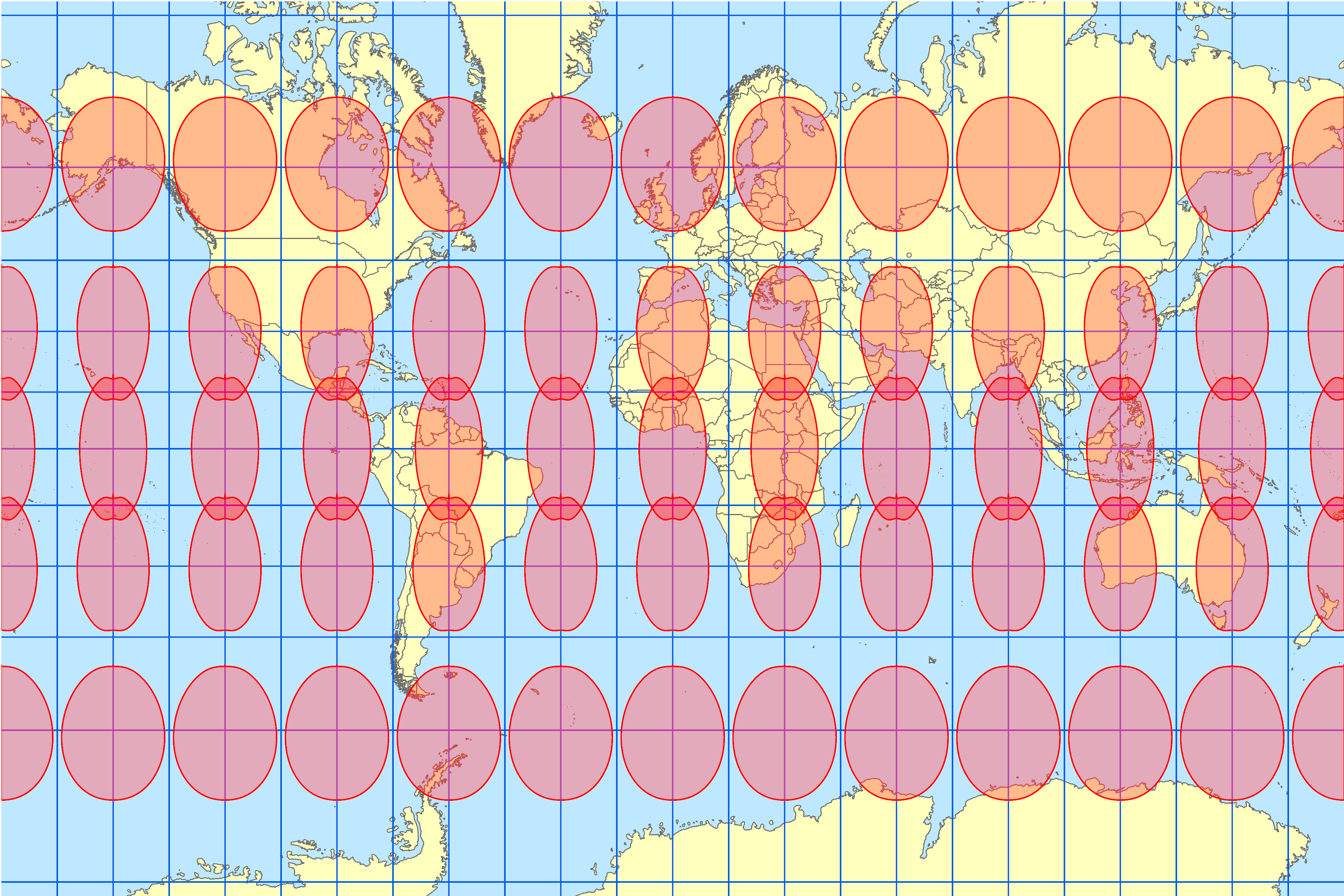
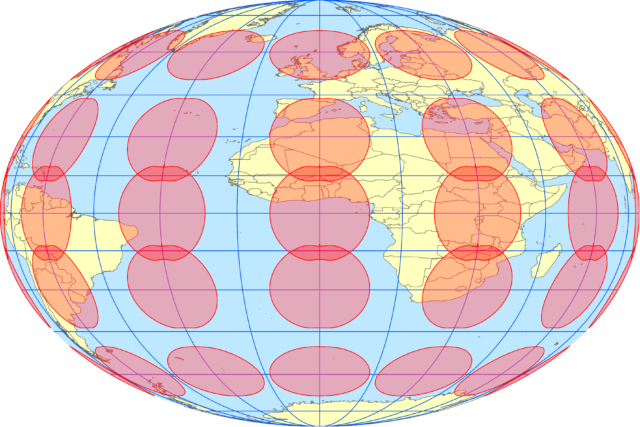
今回のトピックである Webメルカトルで表現するとこのようになります。円の形状が楕円になっています。
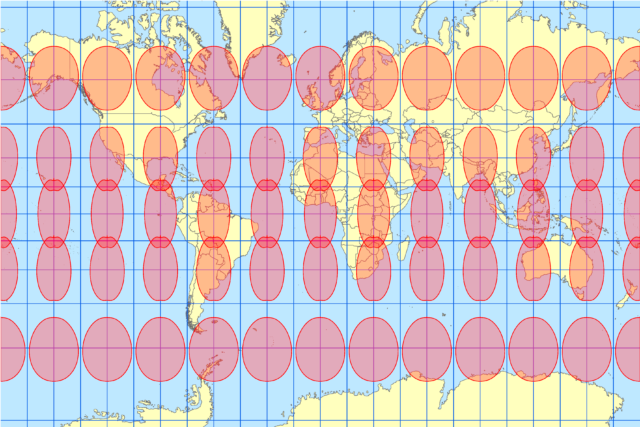
大陸の形は、普段よくみるメルカトル図法と同じ表現になりますが、円の形が卵形になっています。これは、Webメルカトルが地球の扁平率を考慮せずに投影しているからです。半径1,000km の円が円の形状を維持できていないので、Webメルカトルは正角ではない、ということになります。
まとめ
Webメルカトル座標系は、正角ではないことを、極端に偏平した準拠楕円体を使って検証してみました。
この話をすると、「Webメルカトルは正方形のタイルが前提だから」と言われることがありますが、座標系とタイルは関係ありません。タイルを正方形で表現したいのなら、切り取る緯度をずらせばよいのです。当時の Google Maps(か前身の会社)の開発部門に、地理学(地図学)に心得がある人がいれば、こんな誤りは防げたのにと、つくづく残念に思います。
実際のズレは緯度0度からの累積であり、大縮尺図で高緯度を拡大した際に赤道が表現されることはないため、地図上の相対的な位置関係でとらえると大きな問題にはならないのですが、2005年に GIS のプロ達は Google Maps の仕様に困り果てていました。
権力があれば実際の地球の表現も変えてしまう。これはTOマップでお馴染みの、中世におけるキリスト教の世界観です。ギリシャ文明で栄えた科学が中世になり逆行したように、Webメルカトルの登場によって、民衆に対する地図の理解は大きく逆行したと考えています。
地理院地図の前身であるウォッちずは、全国をランベルト正角円錐図法で表現していました。その名残として、初期の地理院地図では画像を引き伸ばしただけなので、ランベルト正角円錐図法では平行に表現されていた注記がメルカトル図法に投影変換されることで扇形になっていた時期がありました。巨人の手にかかれば、一国家の測量機関さえも従わせることができるのです。
こんな記事を書いていると、そのうち弾劾裁判にかけられて火刑になるかもしれませんが、私は「それでも地球は偏平している」と言い続けます。